西門子CPU模塊6ES7318-3EL01-0AB0

1,、線性性

【元件的線性性】當(dāng)描述元件的特性方程為線性方程時(shí),，元件為線性元件,，如線性電阻元件有的特性方程,，線性受控源（CCVS）,。

【線性電路】 除電源,。>獨(dú)立電源外,，電路中的其他元件均為線性元件,，這種電路稱為線性電路

【線性時(shí)不變電路】除獨(dú)立電源外,，電路中其他元件均為線性元件,，且是時(shí)不變?cè)@種電路稱為線性時(shí)不變電路,。

【電路的線性性】線性電路中,，響應(yīng)（電路中的任何電壓或電流）和激勵(lì)（獨(dú)立電壓源與獨(dú)立電流源）的關(guān)系為線性關(guān)系。線性關(guān)系體現(xiàn)為可加性和齊次性,。

【齊次性】 在僅有一個(gè)獨(dú)立電源激勵(lì)的線性電路中,，若將激勵(lì)增大K倍，響應(yīng)也相應(yīng)增大K倍,，如圖4-1-1所示,，如果激勵(lì)下的某個(gè)響應(yīng)（電路中的任何電壓或電流）為,，則激勵(lì)下的某個(gè)響應(yīng)為,。

【可加性】 多個(gè)激勵(lì)共同作用引起的響應(yīng),，等于每個(gè)激勵(lì)單獨(dú)作用所引起的響應(yīng)之和,。如圖4-1-2所示,，如果激勵(lì)下的某個(gè)響應(yīng)為,，激勵(lì)下的某個(gè)響應(yīng)為,，則和共同激勵(lì)下的響應(yīng)為,。

2、疊加定理

【疊加定理】 對(duì)于任意線性電路，由多個(gè)獨(dú)立電源共同作用所引起的響應(yīng)等于這些獨(dú)立電源分別單獨(dú)作用時(shí)所引起的響應(yīng)的代數(shù)和,。疊加定理是線性電路的線性性質(zhì)的體現(xiàn),。

【例4-1-1】 應(yīng)用疊加定理計(jì)算圖4-1-3（a）中電流和電壓。

解 圖4-1-3（a）所示電路有一個(gè)獨(dú)立電壓源和一個(gè)獨(dú)立電流源,，兩個(gè)電源共同作用下的響應(yīng)可以由結(jié)點(diǎn)分析方程求得。即

解得                      

則電流為                

通過(guò)疊加定理分析,。獨(dú)立電源分別單獨(dú)作用的電路如圖4-1-3（b）,、（c）所示,。電壓源單獨(dú)作用電路如圖4-1-4（b）所示，有

,，

電流源單獨(dú)作用電路如圖4-1-3（c）所示,，有

，

根據(jù)疊加定理

可見(jiàn),，兩電源共同作用的響應(yīng)是兩電源單獨(dú)作用時(shí)響應(yīng)之和,。本例的結(jié)果證明了疊加定理的結(jié)論。

【例4-1-2】 應(yīng)用疊加定理計(jì)算圖4-1-4（a）所示電路中的電壓u,。并確定40Ω電阻消耗的功率,。

解 本例若采用結(jié)點(diǎn)分析法,，要建立兩個(gè)結(jié)點(diǎn)方程,，求解方程工作量不大，應(yīng)該優(yōu)先選擇結(jié)點(diǎn)分析,。用疊加定理分析時(shí),，獨(dú)立電源分別作用的電路如圖4-1-4（b）、（c）,、（d）所示,，三個(gè)電路的分析均可以采用分壓、分流關(guān)系實(shí)現(xiàn),，計(jì)算工作量也不太大,，可以選擇疊加定理來(lái)分析。根據(jù)疊加定理,，,。

按照電阻串聯(lián)、并聯(lián)和分壓關(guān)系,，不難得到

圖（d）中,， 10Ω和40Ω電阻并聯(lián)，結(jié)果為8Ω電阻,，兩個(gè)8Ω電阻串聯(lián),，再和2Ω并聯(lián)，由分流關(guān)系不難得到

因此                     

功率               

但,，即功率不符合疊加定理,。

【例4-1-3】電路如圖4-1-5（a）所示，試用疊加定理求受控電源端電壓U及其提供的功率,。

解 本例分析方法應(yīng)該是結(jié)點(diǎn)法，為了說(shuō)明受控電源在疊加定理應(yīng)用時(shí)的處理方法,，在此用疊加定理分析,。用疊加定理分析含受控電源電路時(shí)，受控電源保留在獨(dú)立電源單獨(dú)作用的各電路之中,。電壓源和電流源分別單獨(dú)作用的電路如圖4-1-5（b）和（c）所示,。

圖4-1-5（b）中，由KCL和KVL分別得到

解得                               

圖 4-1-6（c）中,，由KCL和KVL分別得到

解得                             

當(dāng)兩電源共同作用時(shí),，     

受控電源提供的功率為           

【疊加定理應(yīng)用注意事項(xiàng)】

1.      疊加定理僅適用于線性電路。

2.      應(yīng)用疊加定理分析含受控源電路時(shí),，通常不把受控源單獨(dú)作用于電路,，而把受控源作為電阻元件一樣對(duì)待，當(dāng)某一獨(dú)立電源單獨(dú)作用時(shí),，受控源保留在電路中,。

3.      疊加時(shí)應(yīng)注意各響應(yīng)分量的參考方向與原來(lái)的響應(yīng)變量方向是否一致，方向一致則響應(yīng)分量前應(yīng)取“+"號(hào),，不一致則響應(yīng)分量前應(yīng)取“－"號(hào)

西門子CPU模塊6ES7318-3EL01-0AB0

第 1 節(jié) 疊加定理和齊次定理

一,、疊加定理

圖 4.1-1 （ a ）所示電路中，有兩個(gè)激勵(lì),，即獨(dú)立電壓源 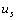和獨(dú)立電流源 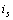,，現(xiàn)欲求 R1 支路上的電流 。

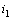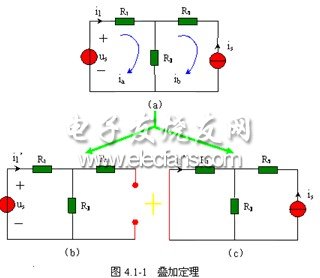
用網(wǎng)孔電流法求解,。設(shè)網(wǎng)孔電流分別為 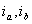，其方向都為順時(shí)針?lè)较?，如圖 4.1-1 （ a ）所示,。網(wǎng)孔方程為

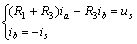
解方程得，網(wǎng)孔電流為

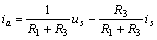
所以,， R1 支路電流為

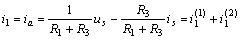
其中,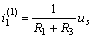， 可以看成是當(dāng) 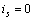時(shí)的 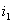的值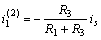， 則可看成是當(dāng) 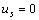時(shí)的 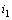的值,。如圖 4.1-1 （ b ）,、（ c ）,。

令

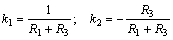
則

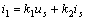
其中,， k1 ,， k2 是由電路的結(jié)構(gòu)和元件的參數(shù)決定的,。對(duì)于線性電路,， R1 、 R2 ,、 R3 都是常數(shù),，不會(huì)隨著電路中激勵(lì)的數(shù)目和大小的改變而改變，所以 k1 ,， k2 也不會(huì)隨激勵(lì)的改變而改變,，即為常數(shù)。 i 是激勵(lì)的一次線性函數(shù),。

疊加定理

（ superposition theorem ）

由線性元件組成的線性電路,，當(dāng) n 個(gè)激勵(lì)共同作用時(shí)，在某條支路上產(chǎn)生的響應(yīng),，等于各個(gè)激勵(lì)單獨(dú)作用時(shí)產(chǎn)生的響應(yīng)的代數(shù)和,。

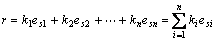
其中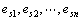， 表示 n 個(gè)激勵(lì)（獨(dú)立電壓源或獨(dú)立電流源）,， r 表示某條支路上產(chǎn)生的響應(yīng)（電壓或電流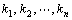）。 都是常數(shù),，其大小由電路的結(jié)構(gòu)和元件的參數(shù)決定。

應(yīng)用疊加定理時(shí)應(yīng)注意的問(wèn)題

1 ．疊加定理是線性電路的一個(gè)重要性質(zhì),，因此只適用于線性電路，對(duì)于非線性電路則不能使用,。

2 ．當(dāng)某個(gè)激勵(lì)單獨(dú)作用時(shí)，其他激勵(lì)均取 0 ,。將獨(dú)立電壓源取 0 ，是把電壓源短路，將獨(dú)立電流源取 0 是把電流源開路,。

3 ．受控源雖然帶有電源的性質(zhì),，但不直接起激勵(lì)作用，因此,，在疊加定理中,，受控源一般不單獨(dú)作用，而是把受控源當(dāng)電路元件處理,。當(dāng)獨(dú)立源單獨(dú)作用時(shí)，受控源應(yīng)保留在電路中,。

4 ．疊加定理只適用于計(jì)算電壓或電流，而不適用于計(jì)算功率,，因?yàn)楣β逝c電壓,、電流之間的關(guān)系不是線性關(guān)系。

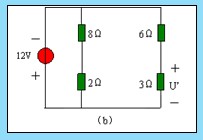
例 4.1-1 圖 4.1-2 （ a ）所示電路,，試用疊加定理求 3 Ω電阻上的電壓 U 及功率,。

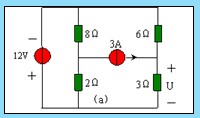
解：電路中有兩個(gè)獨(dú)立源共同激勵(lì),。

1 、當(dāng) 12V 電壓源單獨(dú)激勵(lì)時(shí),，電流源應(yīng)視為 0 ，即把電流源開路,，如圖 4.1-2 （ b ）所示,。

由分壓公式，得

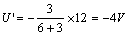
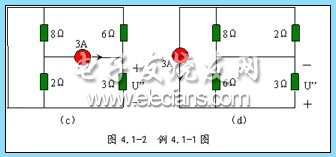
2 ,、當(dāng) 3A 電流源單獨(dú)激勵(lì)時(shí)，電壓源應(yīng)視為 0 ,，即把電壓源短路,，如圖 4.1-2 （ c ）所示。對(duì)圖 4.1-2 （ c ）電路作變換,，得圖 4.1-2 （ d ）所示電路,。

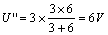
3 ,、當(dāng)電壓源和電流源共同作用時(shí)，由疊加定理得 3 Ω電阻上的電壓

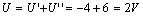
3 Ω電阻上的功率為

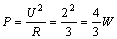
注 意

計(jì)算功率時(shí)，不能用疊加定理,。

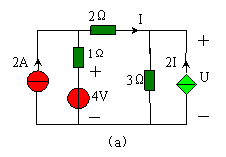
例 4.1-2 用疊加定理計(jì)算圖 4.1-3 （ a ）所示電路中受控源兩端電壓及功率。

解：當(dāng) 4V 電壓源單獨(dú)作用時(shí),，電流源視為開路,，其電路如圖 4.1-3 （ b ）所示，對(duì)圖中所示的回路,，利用 KVL ,，得

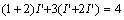
所以,，

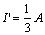
則

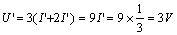
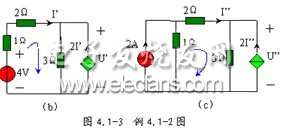
當(dāng) 2A 電流源單獨(dú)作用時(shí),，電壓源視為短路，其電路如圖 4.1-3 （ c ）所示,，對(duì)圖中所示的回路，利用 KVL ,，得

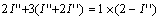
所以,，

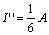
則

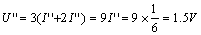
因此,，當(dāng)電壓源和電流源共同作用時(shí),，利用疊加定理得

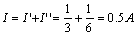
受控源兩端電壓為

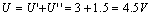
受控源的功率為

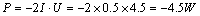
二,、齊次定理

齊次定理

（ homogeneity theorem ）

當(dāng)線性電路中只有一個(gè)獨(dú)立源作用時(shí),，電路的響應(yīng)與激勵(lì)成正比。

推 論：對(duì)于線性電路,，若所有激勵(lì)同時(shí)擴(kuò)大（或縮?。?K 倍，則電路中任一支路的響應(yīng)也擴(kuò)大（或縮?。?K 倍,。

例 4.1-3 圖 4.1-4 所示的梯形電路中， Us=6V ,，試用齊次定理計(jì)算支路電流 I5 ,。

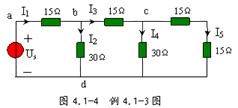
解：這個(gè)電路是由電阻的串、并聯(lián)組成,，可以用等效電路的分析方法進(jìn)行計(jì)算,，但是用齊次定理計(jì)算會(huì)更方便。先設(shè) I5 支路電流為 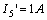,，則

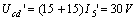
所以,，

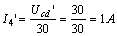
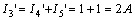
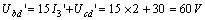
故

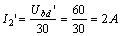
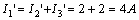
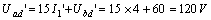
根據(jù)齊次定理，激勵(lì) 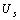與響應(yīng) 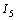成正比,，即

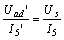
因此,，

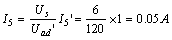
注 意

應(yīng)用疊加定理和齊次定理時(shí)，當(dāng)激勵(lì)的參考方向反向時(shí),，相當(dāng)于激勵(lì)變?yōu)樵瓉?lái)的－ 1 倍,。

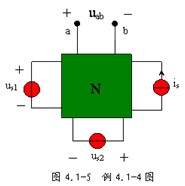
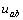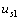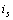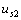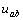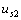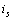例 4.1-4 圖 4.1-5 所示電路中， N 是不含獨(dú)立源的線性網(wǎng)絡(luò),，有 3 個(gè)獨(dú)立源共同激勵(lì),， a 、 b 兩端的電壓 為 10V ,。當(dāng)電壓源 和電流源 反向而 不變時(shí),， 變?yōu)?5V ；當(dāng)電壓源 和電流源 反向而 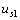不變時(shí),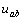， 變?yōu)?3V ,。試問(wèn)：只有電流源 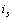反向而電壓源 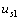和 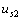不變時(shí)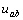， 變?yōu)槎嗌伲?/p>

解：由于是線性電路,，所以可用疊加定理,。 3 個(gè)獨(dú)立源共同激勵(lì),，電路的響應(yīng)

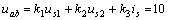（ 1 ）

式中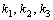， 為常數(shù),，由電路的結(jié)構(gòu)和元件的參數(shù)決定,。

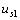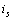當(dāng)電壓源 和電流源 反向而 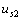不變時(shí)，電路的結(jié)構(gòu)和元件的參數(shù)不變,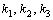， 的大小不變,，而 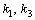都要乘以系數(shù)－ 1 ，這時(shí)的 a ,、 b 兩端的電壓為

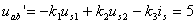（ 2 ）

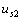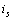又當(dāng)電壓源 和電流源 反向而 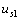不變時(shí)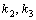， 乘以系數(shù)－ 1 ,， a ,、 b 兩端的電壓為

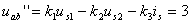（ 3 ）

(2) ＋ (3) ，得

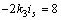（ 4 ）

所以,，當(dāng)只有電流源 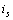反向而電壓源 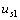和 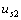不變時(shí),， a 、 b 兩端的電壓為