激光擴束器設計用于擴大平行輸入光束的直徑較大的平行輸出光束,。激光擴束器常用于如激光掃描、干涉測量或遙測應用中?,F(xiàn)在的激光擴束器都是采用從完善的光學望遠鏡基礎中發(fā)展而來的無焦系統(tǒng)設計,。在此類系統(tǒng)中,位于無窮遠的物體光線,,以平行的方式進入內(nèi)部光學件的光軸中,,同時也以平行的方式離開。這意味著整個系統(tǒng)不具備焦距,。
理論:望遠鏡
傳統(tǒng)上,,光學望遠鏡主要用于觀察遠處的目標,例如宇宙中的天體,。光學望遠鏡主要可分為兩大類:折射望遠鏡和反射望遠鏡,。折射望遠鏡充分利用透鏡來折射或彎曲光線,而反射望遠鏡則是利用反射鏡來反射光線,。
折射望遠鏡可分為以下兩類:開普勒式望遠鏡和伽利略式望遠鏡,。開普勒式望遠鏡由焦距為正的透鏡組合而成,而透鏡是通過焦距總和分割(圖1),。離來源圖像或被觀察物體近的透鏡被稱為物鏡,,而靠近人眼或成像的透鏡則成為成像透鏡,。
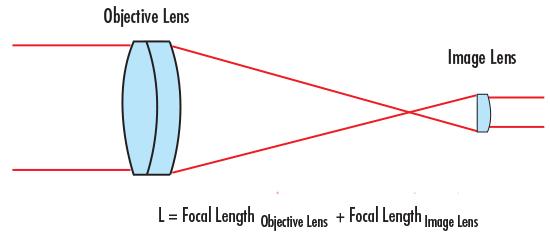
圖1: 開普勒式望遠鏡
伽利略式望遠鏡由正透鏡和負透鏡組合而成,透鏡也是通過焦距總和分割(圖2),。但是,,由于其中一個透鏡為負透鏡,因此兩個透鏡之間的距離比開普勒式望遠鏡的透鏡距離短,。需要注意的是,,使用兩個透鏡之間的有效焦距能夠獲得出色的近似總長度,而使用后焦距則能夠獲得準確的結果,。
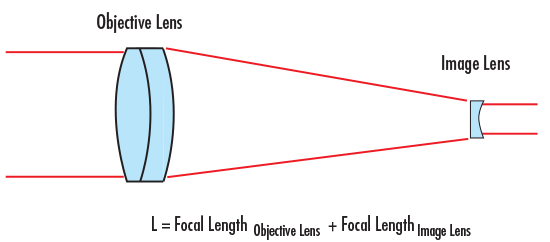
圖2: 伽利略式望遠鏡
望遠鏡的放大倍數(shù)或放大倍數(shù)的倒數(shù)等于物鏡焦距和目鏡焦距的比值,。

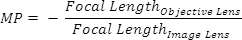
若放大倍數(shù)大于1,則望遠鏡將物體放大,;若放大倍數(shù)小于1,,則望遠鏡將物體縮小。
理論:
在結構中,,物鏡和成像透鏡的位置顛倒,。平行輸入光束在開普勒式中集中在物鏡和成像透鏡之間的一個點上,進而形成一個激光能量聚焦的區(qū)域(圖3),。該集中的點會加熱透鏡之間的空氣,,折射光路中的光線,而這有可能會造成波前誤差,。有鑒于此,,大部分都選擇使用伽利略式設計或其變體(圖4),。

圖3: 開普勒式
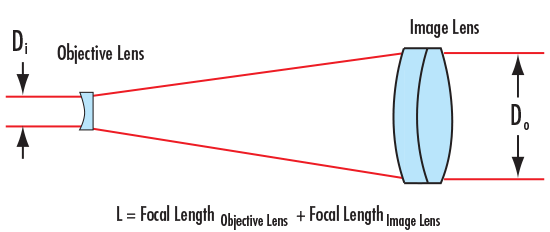
圖4:伽利略式
使用開普勒式或伽利略式設計于應用時,,重要的是能夠計算出輸出光束發(fā)散,這將決定了平行光線的偏差,。光束發(fā)散取決于輸出激光光束直徑和輸出激光光束直徑,。
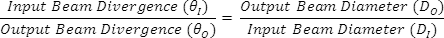
放大倍數(shù)(MP)現(xiàn)在即可依據(jù)光束發(fā)散或光束直徑來表示。
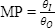
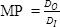
解上述方程式時,,可以看到輸出光束直徑(DO)提高時,,則輸出光束發(fā)散減少,以此類推,。所以,,如果您將來縮小激光光束,光束直徑將會縮小,,但激光的光束發(fā)散將會提高,。小光束的代價就是形成很大的擴張角。
除此之外,,能夠在特定工作距離(L)計算出輸出光束直徑也是極為重要的,。輸出光束直徑是在特定工作距離(L)后輸入光束直徑和光束發(fā)散的函數(shù)(圖5),。

Figure 5: Calculating the Output Beam Diameter at a Specific Working Distance
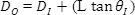
激光光束發(fā)散是以全角的,所以上述方程式是以θI表示,,而非θI/2.,。
由于會隨放大倍數(shù)而提高輸入光束,以及降低輸入光束發(fā)散,,因此將方程式(4)和(5)代入方程式(6)會獲得如下結果,。
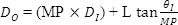
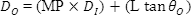
應用示例
示例1
以數(shù)值示例探究先前所述的方程式。
初始參數(shù) 放大倍數(shù) = MP = 10X
輸入光束直徑 = 1mm
輸入光束發(fā)散 = 1mrad
工作距離 = L = 100m
計算參數(shù)
輸出光束直徑
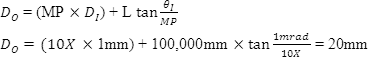
在不具備使用方程式(6)的的情況下,,將此與光束直徑相比較,。
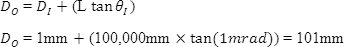
雖然會因特定的擴束功率而提高輸入激光光束,但它也會因相同的擴束功率而降低光束發(fā)散,,進而在較大距離下形成較小的平行光束,。
示例2
使用在長工作距離中降低激光光束發(fā)散的理論示例。
為改善光束準直,,可用于集中激光光束,。下表顯示了5X、10X和20X的的模擬聚焦性能,。光斑尺寸的量度單位為微米,,假設M2=1,使用直徑為0.63mm,,波長為632.8nm的激光光束,,以此計算得出平行的輸入光束。
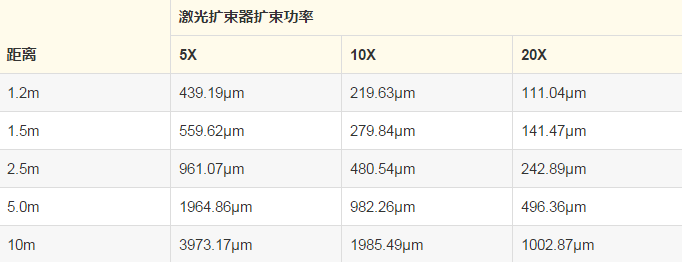
注意:上表所列的1/e2 光斑直徑是從以下方程式計算得出:2 * f/# * 波長,,f/#為工作f/#,。
立即詢價
您提交后,,專屬客服將第一時間為您服務